模数切换
-
符号说明
$\left[x\right]_Q$：表示对整数$x$进行中心模$Q$运算，”中心“指的是需要保证$\left|\left[x\right]_Q\right|\leq Q/2$，这里的$Q$一般是奇数。
$\lceil x \rfloor$：表示四舍五入取整即round。
-
Scale定义：
-
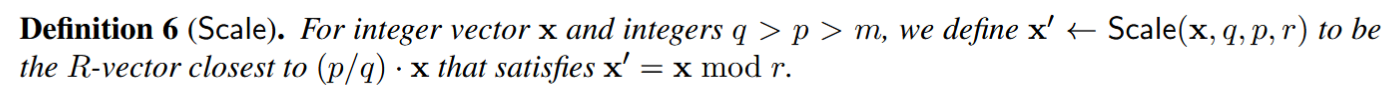
Scale实现：
如果四舍五入时，如果刚好小数位等于0.5，则有两种选择即$x+kr$和$x+(k+1)r$，这时可以随机选择一个或者使用四舍五入选择，当然也可以选择使得最后$[*]_p$之后绝对值较小的那一个。这对于噪声上界估计无明显影响。
- 分析
显然，等号当且仅当$\frac{(p-q)x}{qr}$的小数位$=0.5$时成立。
当然实际使用时，这里$\left|x'-\frac{px}{q}\right|$是可以计算出来的，直接用计算出来的数参与上界估计即可。但是理论分析上界直接使用$r/2$就行了。
-
BGV密文模数切换
设BGV明文模数为$P$，密文初始模数为$Q=Q_L$对于级别$L$，类似级别$t(0\leq t\leq L)$对应$Q_t$，$Q_t=\prod_{i=0}^{t} p_i$
给定一个模数$Q_t$上的BGV密文$c=(c_0,c_1)$，需要将其切换到$Q_{t'}$上的密文$c'=(c_0',c_1')$，其中$t'\lt t$。
注意：$c_i\in Z_{Q_t}[x]/X^N+1$
操作如下：
分析：设私钥为$s$，则BGV公钥加密如下，
$$ b=a\cdot s+P\cdot e_s\\ c_0=b\cdot v+P\cdot e_0+m\\ c_1=-a\cdot v+P\cdot e_1 $$其中$a,b,s,e_s,v,e_0,e_1$都需要满足特定的离散概率分布才能保证安全性。
解密操作为$m=\left[\left[c_0+c_1\cdot s\right]_{Q_t}\right]_P$，$c_0+c_1\cdot s=m+P(e_s\cdot v+e_0+s\cdot e_1)$
令$e=e_s\cdot v+e_0+s\cdot e_1$，则
$$ \begin{aligned} \left|m\right| &\leq P/2\\ \left(c_0,c_1\right)&\rightarrow c_0+c_1\cdot s = m+Pe\\ m&=\left[m+Pe\right]_P=\left[c_0+c_1\cdot s\right]_P\\ \left[\left[c_0\right]_{Q_t}+\left[c_1\cdot s\right]_{Q_t}\right]_{Q_t}&=\left[c_0+c_1\cdot s\right]_{Q_t}=\left[m+Pe\right]_{Q_t}\\ \end{aligned} $$我们需要确保$\left[\left[m+Pe\right]_{Q_t}\right]_P=m$，因此需要满足$\left|m+Pe\right|=\left|c_0+c_1\cdot s\right|\lt Q_t/2$
事实上，这里的$e$可以根据加密参数设置一个上界比如$e_b>0$，需要满足$\left|m+Pe\right|\leq\left|m\right|+P\left|e\right|\lt P/2 +P\left|e\right|\lt Q_t/2$
即$\left|e\right|\leq e_b\lt \frac{Q_t}{2P}-\frac{1}{2}$
又$\left|e\right|=\left|e_s\cdot v+e_0+s\cdot e_1\right|$，所以$\Vert e\Vert_{\infty}\leq \Vert e_s\Vert_2 \Vert v\Vert_2+\Vert e_0\Vert_{\infty}+\Vert s\Vert_2 \Vert e_1\Vert_2$
显然，$e_b$的大小应该和$s,e_s,v,e_0,e_1$的离散概率分布参数有关。
注意，上面的分析是在解密前没有对密文进行运算的前提下展开的，下面分析如果密文参与运算如何解密分析：
$(\left[c_0^*\right]_{Q_t},\left[c_1^*\right]_{Q_t})$，
以加法为例，不妨假设密文$(\left[c_0^0\right]_{Q_t},\left[c_1^0\right]_{Q_t},e_b^0),(\left[c_0^1\right]_{Q_t},\left[c_1^1\right]_{Q_t},e_b^1)$进行加法运算得到
$$ \left(c_0^*=\left[c_0^0\right]_{Q_t}+\left[c_0^1\right]_{Q_t},c_1^*=\left[c_1^0\right]_{Q_t}+\left[c_1^1\right]_{Q_t}\right)\\ \left(\left[c_0^*\right]_{Q_t}=\left[\left[c_0^0\right]_{Q_t}+\left[c_0^1\right]_{Q_t}\right]_{Q_t},\left[c_1^*\right]_{Q_t}=\left[\left[c_1^0\right]_{Q_t}+\left[c_1^1\right]_{Q_t}\right]_{Q_t}\right)\\ c_0^0+c_1^0\cdot s = m^0+Pe^0,\left|e^0\right|\leq e_b^0\\ c_0^1+c_1^1\cdot s = m^1+Pe^1,\left|e^1\right|\leq e_b^1\\ c_0^*+c_1^*\cdot s = \left[c_0^0\right]_{Q_t}+\left[c_0^1\right]_{Q_t}+\left[c_1^0\right]_{Q_t}\cdot s+\left[c_1^1\right]_{Q_t}\cdot s\\ \left[c_0^*\right]_{Q_t}+\left[c_1^*\right]_{Q_t}\cdot s = \left[c_0^0+c_0^1\right]_{Q_t}+\left[c_1^0+c_1^1\right]_{Q_t}\cdot s\\ \left[\left[c_0^*\right]_{Q_t}+\left[c_1^*\right]_{Q_t}\cdot s\right]_{Q_t}= \left[\left[c_0^0+c_0^1\right]_{Q_t}+\left[c_1^0+c_1^1\right]_{Q_t}\cdot s\right]_{Q_t} =\left[c_0^0+c_0^1+(c_1^0+c_1^1)\cdot s\right]_{Q_t}=\left[(m^0+m^1)+P(e^0+e^1)\right]_{Q_t} $$我们显然期待$\left[\left[(m^0+m^1)+P(e^0+e^1)\right]_{Q_t}\right]_P=\left[m^0+m^1\right]_P$
由前面的分析，可知，需要保证$\left|e^0+e^1\right|\lt \frac{Q_t}{2P}-\frac{1}{2}$，只需要$e_b^0+e_b^1\lt \frac{Q_t}{2P}-\frac{1}{2}$即可。
这也是为什么经常说加法的噪声是累加的。
推广：
$\left[\left[f\left(m^0,m^1,\dots,m^k\right)+Pg\left(e^0,e^1,\dots,e^k\right)\right]_{Q_t}\right]_P=\left[f\left(m^0,m^1,\dots,m^k\right)\right]_P$
成立的条件是$\left|g\left(e^0,e^1,\dots,e^k\right)\right|\lt \frac{Q_t}{2P}-\frac{1}{2}$
通过各种不等式放缩，一般可以得到$\left|g\left(e^0,e^1,\dots,e^k\right)\right|\leq h(e_b^0,e_b^1,\dots,e_b^k)\lt \frac{Q_t}{2P}-\frac{1}{2}$
模数切换成立的条件是解密后对应的明文相同，因此可以对应三个充分条件：
- (1) $c_0'=\text{Scale}(c_0),\;c_1'=\text{Scale}(c_1)$
- (2) $Q_t\equiv Q_{t'}\equiv 1(\text{mod}\; P)$
- (3) $\frac{Q_{t'}}{Q_t}\left(P/2+Pe_b\right)+P/2+P\sqrt{N}\Vert s\Vert_2/2\leq Q_{t'}/2$
证明：
$$ \begin{aligned} c_0[j]+(c_1\cdot s)[j]&=M+k[j]Q_t,\left|M\right|\lt Q_t/2\\ c_0'[j]+(c_1'\cdot s)[j]&=M+k[j]Q_t+r[j]P\\ c_0'[j]+(c_1'\cdot s)[j]&=M'+k'[j]Q_{t'},\left|M'\right|\lt Q_{t'}/2\\ M+k[j]Q_t+r[j]P&=M'+k'[j]Q_{t'}\\ M+k[j]Q_t+r[j]P&=M'+k'[j]Q_{t'}(\text{mod}\;P)\\ M+k[j]&\equiv M'+k'[j](\text{mod}\;P)\\ \end{aligned} $$显然只需要说明$k[j]=k'[j]$，即可得到$M\equiv M'(\text{mod}\;P)$，因此对应明文相同。
证明$k=k'$等价于证明当$k=k'$时有$\left|M'\right|\lt Q_{t'/2}$成立即$\left|c_0'[j]+(c_1'\cdot s)[j]-k[j]Q_{t'}\right|\lt Q_{t'}/2$
直接代入验证，令 $M^*[j]=c_0'[j]+(c_1'\cdot s)[j]-k[j]Q_{t'}$，则
$$ \begin{aligned} M^*[j]&=c_0'[j]-Q_{t'}c_0[j]/Q_t+Q_{t'}c_0[j]/Q_t+(c_1'\cdot s)[j]+(Q_{t'}c_1/Q_t\cdot s)[j]-(Q_{t'}c_1/Q_t\cdot s)[j]-k[j]Q_{t'}\\ &=(-k[j]Q_{t'}+Q_{t'}c_0[j]/Q_t+(Q_{t'}c_1/Q_t\cdot s)[j])\\ &+c_0'[j]-Q_{t'}c_0[j]/Q_t\\ &+(c_1'\cdot s)[j]-(Q_{t'}c_1/Q_t\cdot s)[j]\\ &=Q_{t'}M[j]/Q_t\\ &+c_0'[j]-Q_{t'}c_0[j]/Q_t\\ &+((c_1'-Q_{t'}c_1/Q_t)\cdot s)[j] \end{aligned} $$只需要说明此时的$\left|M^*[j]\right|\lt Q_{t'}/2 $即$M^*=M'$。
多项式乘法的系数上界可以由柯西-施瓦茨不等式确定，$\left|(c\cdot s)[j]\right|\leq \Vert c\Vert_2\Vert s\Vert_2$
所以$\left|((c_1'-Q_{t'}c_1/Q_t)\cdot s)[j]\right|\leq \Vert(c_1'-Q_{t'}c_1/Q_t)\Vert_2\Vert s\Vert_2$
因为$\left|c_i'[j]-Q_{t'}c_i[j]/Q_t)\right|\leq P/2$，所以$||(c_i'-Q_{t'}c_i/Q_t)||_2\leq P\sqrt{N}/2$
因此
$$ \begin{aligned} \left|M^*[j]\right|&\leq \frac{Q_{t'}}{Q_t}\left|M[j]\right|+P/2+P\sqrt{N}\Vert s\Vert_2/2 \end{aligned} $$显然，如果控制$\left|M[j]\right|$和$\Vert s\Vert_2$的上界不太大，是可以做到$\left|M^*[j]\right|\lt Q_{t'}/2$的，此时$M^*=M'$。注意到，如果$\left|M^*[j]\right|\lt Q_{t'}/2$，则必须要求$\left|M[j]\right|\lt Q_t/2$，这是必然的。
因为$\left|M[j]\right|\lt P/2 +Pe_b$，所以只需要$\frac{Q_{t'}}{Q_t}\left(P/2+Pe_b\right)+P/2+P\sqrt{N}\Vert s\Vert_2/2\leq Q_{t'}/2$即可，这就是条件(3)。
证毕。
-
噪声
$$ \begin{aligned} e'&=\frac{M'-m}{P}\\&=\frac{Q_{t'}M[j]/Q_t+(c_0'-Q_{t'}c_0/Q_t)+\left(\left(c_1'-Q_{t'}c_1/Q_t\right)\cdot s\right)-m}{P}\\ &=\frac{Q_{t'}}{Q_t}\frac{M[j]-m}{P}+\frac{(c_0'-Q_{t'}c_0/Q_t)+\left(\left(c_1'-Q_{t'}c_1/Q_t\right)\cdot s\right)}{P}+(\frac{Q_{t'}}{Q_t}-1)\frac{m}{P}\\ &=\frac{Q_{t'}}{Q_t}e+\frac{(c_0'-Q_{t'}c_0/Q_t)+\left(\left(c_1'-Q_{t'}c_1/Q_t\right)\cdot s\right)}{P}+(\frac{Q_{t'}}{Q_t}-1)\frac{m}{P} \end{aligned} $$$$ \begin{aligned} \left|e'\right|&\leq \left|\frac{Q_{t'}}{Q_t}e\right|+\left|\frac{(c_0'-Q_{t'}c_0/Q_t)+\left(\left(c_1'-Q_{t'}c_1/Q_t\right)\cdot s\right)}{P}\right|+\left|(\frac{Q_{t'}}{Q_t}-1)\frac{m}{P}\right| \\ &\leq \frac{Q_{t'}}{Q_t}\left|e\right|+\frac{1}{2}+\frac{\sqrt{N}\Vert s\Vert_2}{2}+1-\frac{Q_{t'}}{Q_t} \\ &=\frac{Q_{t'}}{Q_t}\left|e\right|+\frac{\sqrt{N}\Vert s\Vert_2}{2}+\frac{3}{2}-\frac{Q_{t'}}{Q_t} \\ &\approx \frac{Q_{t'}}{Q_t}\left|e\right|+\frac{\sqrt{N}\Vert s\Vert_2}{2} \\ &\leq \frac{Q_{t'}}{Q_t}e_b+\frac{\sqrt{N}\Vert s\Vert_2}{2} \end{aligned} $$所以$e_b'=\frac{Q_{t'}}{Q_t}e_b+\frac{\sqrt{N}\Vert s\Vert_2}{2}$。
-
如何设置噪声和私钥的上界是核心问题，太大了会导致支持的级别变少。当然此时安全性也会发生变化。
-
还有我这里是逐个元素进行绝对值判断，也可以从向量的角度进行范数分析，比如无穷范数/欧几里得范数/嵌入范数等等。
拓展1
我们不再限制$Q_t\equiv 1(\text{mod}\;P)$，只要求$\text{gcd}(Q_t,P)=1$。
-
Scale_new
令$Q_{t'}c_i=Q_ta_i+b_i,\left|b_i\right|\leq Q_t/2$，$Q_td_i\equiv b_i(\text{mod}\;P),\left|d_i\right|\leq P/2$，则
$$ c'_i=a_i+d_i $$ -
新的公钥加解密操作如下：
（1）加密
令$k_t =\left[Q_t\right]_P,\hat{m}=\left[m\cdot k_t\right]_P$
$$ b=a\cdot s+P\cdot e_s\\ c_0=b\cdot v+P\cdot e_0+\hat{m}\cdot Q_t\\ c_1=-a\cdot v+P\cdot e_1 $$（2）解密
$$ \hat{m}=\left[\left[c_0+c_1\cdot s\right]_{Q_t}\right]_P\\ m=\left[\hat{m}\cdot k_t^{-1}\right]_P $$重写上述证明如下：
$$ \begin{aligned} c_0[j]+(c_1\cdot s)[j]&=M+k[j]Q_t,\left|M\right|\lt Q_t/2\\ c_0'[j]+(c_1'\cdot s)[j]&=M'+k'[j]Q_{t'},\left|M'\right|\lt Q_{t'}/2\\ \end{aligned} $$此时我们不需要证明$M\equiv M'(\text{mod}\;P)$，而是要证明$M\cdot Q_t^{-1}\equiv M'\cdot Q_{t'}^{-1}(\text{mod}\;P)$即$M\cdot Q_{t'}\equiv M'\cdot Q_t(\text{mod}\;P)$。也就是要验证
$$ (c_0[j]+(c_1\cdot s)[j]-k[j]Q_t)Q_{t'}=(c_0'[j]+(c_1'\cdot s)[j]-k'[j]Q_{t'})Q_{t}(\text{mod}\;P)\\ (c_0[j]+(c_1\cdot s)[j])Q_{t'}-k[j]Q_tQ_{t'}=(c_0'[j]+(c_1'\cdot s)[j])Q_{t}-k'[j]Q_tQ_{t'}(\text{mod}\;P) $$由Scale_new操作可得，
$$ Q_{t'}c_i=Q_ta_i+b_i\\ Q_{t'}c_i\equiv Q_ta_i+Q_td_i(\text{mod}\;P)\\ Q_{t'}c_i\equiv Q_t(a_i+d_i)(\text{mod}\;P)\\ Q_{t'}c_i\equiv Q_tc_i'(\text{mod}\;P)\\ $$所以和前面的证明类似，我们只需要说明$k[j]=k'[j]$即可。
类似的，还是带入$k$计算$M^*$，结果和前面一样，噪声分析时的唯一一点区别在于：$\left|c_0'[j]-Q_{t'}c_0[j]/Q_t)\right|\leq P/2$这个上界不严格成立了，需要重新估计。
$$ c_0'[j]-Q_{t'}c_0[j]/Q_t=a_0+d_0-Q_{t'}c_0/Q_t=d_0-b_0/Q_t $$因为$\left|d_0\right|\leq P/2,\left|b_0/Q_t\right|\leq 1/2$，所以
$$ \left|d_0-b_0/Q_t\right|\leq \left|d_0\right|+\left|b_0/Q_t\right|\leq \frac{P+1}{2} $$相当于原来的上界增加1/2，这个几乎可以看做没有增加了。
条件(3)也可以更新为$\frac{Q_{t'}}{Q_t}\left(P/2+Pe_b\right)+\frac{P+1}{2}+(P+1)\sqrt{N}\Vert s\Vert_2/2\leq Q_{t'}/2$
总的来说，用几乎没有增加的上界来放松对$Q_t$的约束，这个改变是非常成功的！！！
当然还有其他的代价，比如需要存储$Q_t(\text{mod}\;P)$和$Q_t^{-1}(\text{mod}\;P)$且加解密都增加额外的乘法操作。
拓展2
拓展1的$Q_t$足够放松了，但是存在一个缺陷，$Q_{t'}c_i=Q_ta_i+b_i,\left|b_i\right|\leq Q_t/2$，这里计算$a_i,b_i$是比较浪费时间的，因此我们对$Q_t$添加·一个约束，令$Q_{t'}|Q_t, t' 我们想保证$Q_{t'}c_i\equiv Q_tc_i'(\text{mod}\;P)$，一个想法是： 令$Q_tc_i'=Q_{t'}(c_i+r_iP)$，这个$r_i$的取值目前还没有确定。 显然，此时有$c_i'=\frac{Q_{t'}(c_i+r_iP)}{Q_t}$。 令$Q_{t'}|Q_t$，则$c_i'=\frac{c_i+r_iP}{R}$ 所以$r_iP\equiv -c_i(\text{mod}\;R)$ 因为$\text{gcd}(P,R)=1$，令$r_i=-c_iP^{-1}(\text{mod}\;R)$。 所以新的scale是 $\left|c_i'-\frac{c_i}{R}\right|=\left|\frac{\left(-c_iP^{-1}\left(\text{mod}\;R\right)\right)P}{R}\right|\leq P/2$ 这是目前看到的三种实现BGV mod-switch的方法，三种方法既有相同之处又有各自的特点，应该根据参数选取，性能，噪声等等指标来权衡使用哪一种方式。注意：拓展2和拓展3是可以一起使用的。
总结